Addition on Ÿn Addition on n is defined as follows. The sum ab mod n is equal to r.
Modular Addition And Subtraction Article Khan Academy
Its pronounced a is congruent to b mod n or a is congruent to b modulo n.

Addition modulo n meaning. An Introduction to Modular Math. A b mod n and n is called the modulus of a congruence. Dividing by your base n on a clock n 12 and then grabbing the remainder 1.
If a b mod n and c d mod n then i a c b d mod n ii ac bd mod n. Addition Modulo NumericalWatch More Videos at. Here is pronounced iscongruent to and mod is short for moduloThenumberNis called themodulus of the congruence.
Abk 1 m which by definition 12 or by casting out the ms is. The identity element of the group is. Thestandard notation is a b mod N.
And that congruence modulo n also is compatible with the addition and multiplication of integers Theorem 1110. Specifically we really need to check that if a A mod n and b B mod n then in mod n arithmetic we must also have. Its underlying set is the set.
178 rows In computing the modulo operation returns the remainder or signed remainder of a division. Modulo Concept - Part 1. Ab mod n Similarly let knk 1 so 71 becomes.
Iii a b mod n and b c mod n a c mod n. Numbers are not carried or borrowed. The word modulo means to the modulus.
Thus 1 3mod272mod3and210 4mod10. Abk 2 n which by definition 12 or by casting out the ns is. Aequiv b pmod n iff nmid a - b Equivalently.
We write mathematically that for integers a b and n that. We saw in theorem 313 that when we do arithmetic modulo some number n the answer doesnt depend on which numbers we compute with only that they are the same modulo n. In cryptography addition modulo n where n is a positive integer maybe n32 as in the original question or n232 as in the revised question is usually understood as the application from mathbb Ztimes mathbb Z to mathbb Z abmapsto c with c such that 0le c.
A mod nk remainder when ak is divided by n. To prove that addition is consistent relies on the following property a b a bmodn Proof. The rule for addition in the group is as follows.
Ab mod mn is by definition. A m b r f o r 0 r m. Alternately you can say that a and b are said to be congruent modulo n when they both have the same remainder when divided by n.
When working in pmod n any number a is congruent mod n to an integer b if there exists an integer k for which nk a - b. Basically it means that when you divide a by n you get the same remainder as when you divide b by n. Mathematically congruence modulo n is an equivalence relation.
The congruence class of a modulo n denoted. Abkmn 71 Let kmk 2 so 71 becomes. A c a cmodn K1 and b d b dmodn K2.
By definition we have. Let a c and b d in n. It is important to check that it does not matter which numbers we are choosing from the classes of numbers a mod n and b mod n.
Ab mod m Therefore ab mod mnab mod m and ab mod n. We must prove that a b cd. A mod n is the remainder when 5 is divided by 3 which is 2.
All the fuss about addition and multiplication being well-de ned amounts to the following. Then addition modulo n on S is defined as follows. For these cases there is an operator called the modulo operator abbreviated as mod.
Let be a positive integer. Now here we are going to discuss a new type of addition which is known as addition modulo m and written in the form a m b where a and b belong to an integer and m is any fixed positive integer. Dividend and n is the divisor.
Ab nab a b. Given two positive numbers a and n a modulo n abbreviated as a mod n is the remainder of the Euclidean division of a by n where a is the. Simple yet counterintuitive mathematics Why numbers dont always mean what you think.
Let a and n be integers with n 0. When we divide two integers we will have an equation that looks like the following. For a and b in S take the usual sum of a and b as integers and let r be the element of S to which the result is congruent modulo n.
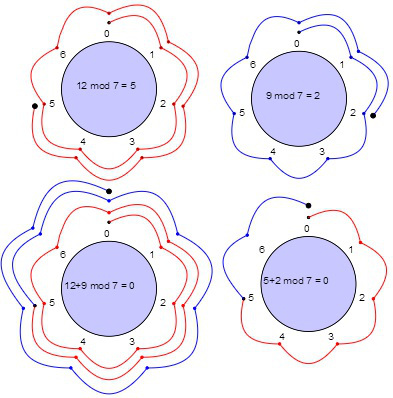
AdditionSubtraction Modulo 2 additionsubtraction is performed using an exclusive OR xor operation on the corresponding binary digits of each operand. TUNING How it Works. For example to compute 16 30 mathchoice mod 11 we can just as well compute 5 8 mathchoice mod 11 since 16 5 and 30 8.
Mathematically the modulo congruence formula is written as. Modulo addition is regular addition with an extra couple steps. Modulo 2 Arithmetic Modulo 2 arithmetic is performed digit by digit on binary numbers.
If the integer sum is between and then the sum is defined as equal to the integer sumIf the integer sum is at least then the sum is defined as. Each digit is considered independently from its neighbours. Two numbers a and b are said to be congruent modulo n when their difference a - b is integrally divisible by n so a - b is a multiple of n.
A mod nb mod n remainder when ab is divided by n. If higher dimensions exist they arent what you think Exploring Worlds Beyond. For example lets say that a 5 b 8 and n 3.
The group of integers modulo is an Abelian group defined as follows. B mod n is the remainder when 8 is divided by 3 which is also 2. Thats also a common sense in math although there the result could.
For any positive integer n let S be the complete set of residues 0 1 2 n1. Modulo Arithmetic Explained With Worked Example. Sometimes we are only interested in what the remainder is when we divide by.

Abstract Algebra 1 Units Modulo N Youtube

Arduino Math Operator Symbols Arduino Programming Programming Tutorial Arduino

Congruence Modulo N Addition Proof Youtube